Dielectric Sphere in External Electric Field

Theoretical Context

When it comes to studying electric fields in matter, we distinguish between two classes of matter: conductors and dielectrics (or insulators). In conductors, about one or two electrons per atom are not associated with any particular nucleus, but they roam around freely, constituting a huge amount of free charge. In dielectrics, on the other hand, all charges are attached to specific atoms or molecules. The only thing these charges can do is move within the atom or molecule.

Under the influence of an external electric field, the free charge in a conductor starts to move freely so as to produce an induced electric field that completely cancels the external electric field. In a dielectric, however, the charges have limited freedom to move, and the cancellation of the external field is incomplete, yielding an overall electric field inside the dielectric that is weaker than the external field, but non-zero.

Video Animation

Interaction of a dielectric sphere of radius

R\equiv 1

with an external electric field.

Slideshow

1: Initially, the dipoles inside the dielectric sphere are randomly oriented.
2: The dipoles align with the external field under its influence.
3: This alignment leads to bound surface charge.
4: The bound surface generates an induced field, which opposes the external field inside the sphere and acts as a dipole field outside the sphere.
5: The external and induced field yield a netto field.

Physical Interpretation

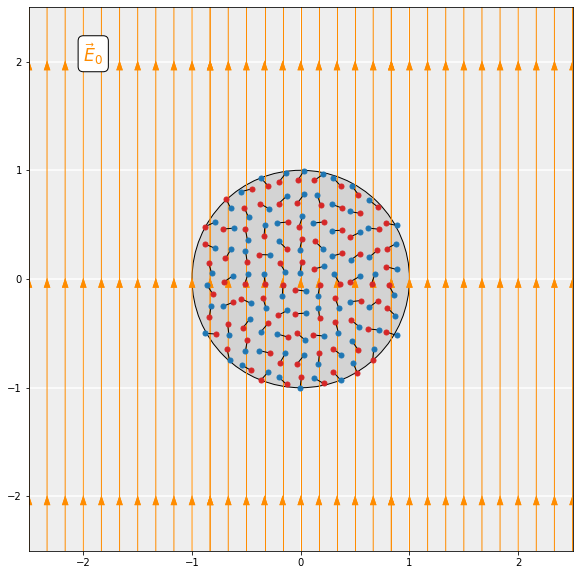
In the animation (and slideshow), we aim to show visually what happens when a dielectric sphere of radius $R$ interacts with a uniform external electric field $\boldsymbol{E}_0$ . We assume that the atoms inside the dielectric act as tiny dipoles with dipole moment $\boldsymbol{p}$ . In the absence of an electric field, the dipoles are randomly oriented within the sphere (slide 1). The dipoles experience a torque $\boldsymbol{\tau}$ due to the presence of the electric field:

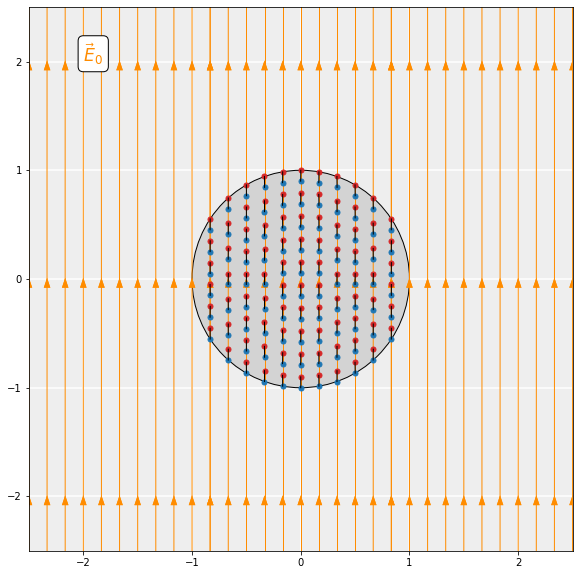
\begin{equation*} \boldsymbol{\tau}=\boldsymbol{p}\times\boldsymbol{E}_0. \end{equation*}

This torque acts to align the dipoles with the electric field (slide 2). In other words, under the influence of the external field, the dipoles start to rotate. In addition to rotation, the dipoles can also stretch, but we neglect this type of movement here. All the microscopic dipoles pointing along the direction of the field result in the macroscopic polarization of the sphere. The amount of polarization is measured by $\boldsymbol{P}$ , the dipole moment per unit volume. Assuming the material is a linear dielectric, the polarization is proportional to the external electric field:

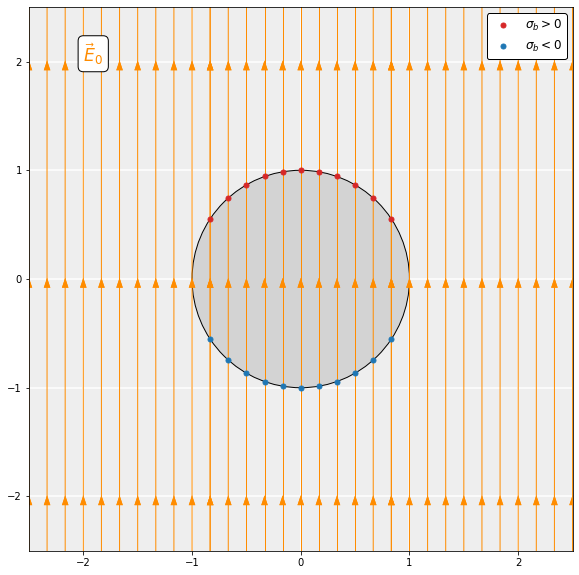
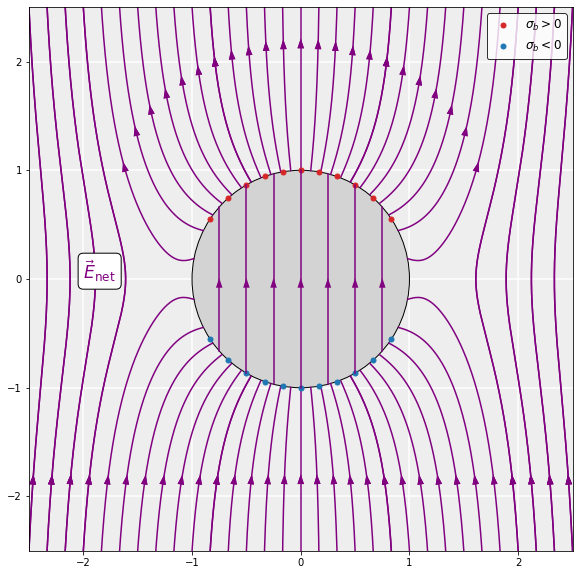
\begin{equation*} \boldsymbol{P} = \epsilon_0\chi_e\boldsymbol{E}_0. \end{equation*}

The polarization results in bound surface charge (slide 3). Inside the sphere ( $r<R$ ), the dipoles line up in the direction of the external field. In doing so, the positive charge on heads and negative charge on tails of neighboring dipoles effectively cancel each other out. However, on the surface of the sphere ( $r=R$ ), this cancellation cannot take place since there are no neighboring dipoles anymore. The surface of the upper hemisphere becomes positively charged and the lower becomes negatively charged: the sphere becomes polarized. The accumulation of charge on the surface is called bound surface charge:

\begin{equation*} \sigma_b = \boldsymbol{P}\cdot\hat{\boldsymbol{n}}=P\cos\theta, \end{equation*}

where $\hat{\boldsymbol{n}}$ is the unit vector pointing away from the sphere and $\theta$ is the angle with vertical.

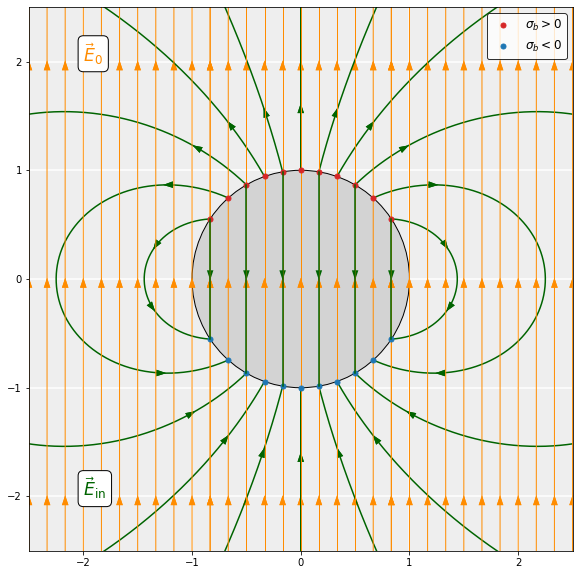
The bound surface charge (or, ultimately the polarization) generated by the external field induces an additional electric field $\boldsymbol{E}_\mathrm{in}$ , called the induced field (slide 4). Inside the sphere, this induced field is uniform and opposes the direction of the external field. The (magnitude of the) induced field is proportional to that of the external field, which can be expressed as:

\begin{equation*} \boldsymbol{E}_\mathrm{in}=-\alpha\boldsymbol{E}_0,\quad\quad\quad (r < R) \end{equation*}

where the dimensionless parameter $\alpha<1$ depends on the properties of the dielectric. The net field inside the sphere is then (slide 5):

\begin{equation*} \boldsymbol{E}_\mathrm{net}=\boldsymbol{E}_0+\boldsymbol{E}_\mathrm{in}=(1-\alpha)\boldsymbol{E}_0<\boldsymbol{E}_0.\quad\quad\quad (r < R) \end{equation*}

The fact that the total field is smaller than the external field inside the sphere but non-zero reflects the fact that the cancellation of the external field inside a dielectric is incomplete.

Outside the sphere, the induced field is simply that of a perfect dipole located at the center of the sphere with dipole moment $\boldsymbol{p}\equiv(4\pi R^3/3)\boldsymbol{P}$ , where $R$ is the radius of the sphere (slide 5). That is:

\begin{equation*} \boldsymbol{E}_\mathrm{in}=\boldsymbol{E}_\mathrm{dip} \equiv \frac{p}{4\pi\epsilon_0r^3}\;(2\cos\theta\;\hat{\boldsymbol{r}}+\sin\theta\;\hat{\boldsymbol{\theta}}).\quad\quad\quad(r > R) \end{equation*}

The net field outside the sphere is then given by:

\begin{equation*} \boldsymbol{E}_\mathrm{net}=\boldsymbol{E}_0+\boldsymbol{E}_\mathrm{dip}.\quad\quad\quad (r > R) \end{equation*}

Just outside the sphere, the total field is a superposition of the dipole field and the external field, with the field lines ‘connecting’ to the surface of the sphere. Far away from the sphere ( $r\gg R$ ), the total field reduces to the external field rapidly since the dipole field goes like $\boldsymbol{E}_\mathrm{dip}\propto 1/r^3$ .

Downloads

*.MP4